제어시스템공학-1] Average Filter(평균필터) https://limitsinx.tistory.com/69
[제어시스템공학-2] Moving Average Filter(이동평균필터) https://limitsinx.tistory.com/70
[제어시스템공학-3] Low Pass Filter(저주파 통과필터) https://limitsinx.tistory.com/71
[제어시스템공학-4] Kalman Filter(칼만필터) 개념정리(1) https://limitsinx.tistory.com/72
[제어시스템공학-5] Kalman Filter(칼만필터) 개념정리(2) https://limitsinx.tistory.com/73
[제어시스템공학-6] Kalman Filter(칼만필터) 구현 - 쉬운예제 https://limitsinx.tistory.com/74
[제어시스템공학-7] Kalman Filter(칼만필터) 구현 - 중간예제 https://limitsinx.tistory.com/75
[제어시스템공학-8] Kalman Filter(칼만필터) 구현 - 어려운예제 https://limitsinx.tistory.com/76
[제어시스템공학-9] Kalman Filter(칼만필터) 구현 - 실전예제 https://limitsinx.tistory.com/77
[제어시스템공학-10] Extended Kalman Filter(확장칼만필터) 개념 https://limitsinx.tistory.com/78
[제어시스템공학-11] Extended Kalman Filter(확장칼만필터) 구현 https://limitsinx.tistory.com/79
[제어시스템공학-12] Unscented Kalman Filter(무향칼만필터) 개념 https://limitsinx.tistory.com/80
※이 전글에서 정리한 코드/개념은 재설명하지 않으므로, 참고부탁드립니다
※해당 글은 PC에서 보기에 최적화 되어있습니다.
이전 글에서 UKF에 대해 개념정리를 해보았는데요
이번에는 코드로 직접 구현해보도록 하겠습니다.
예제는 "Extended Kalman Filter 구현"에서 적용해보았던것과 동일합니다. (하기 붙여넣은 내용)
[문제정의] : https://limitsinx.tistory.com/79
지난글에서는 EKF(확장칼만필터)의 개념에 대해 정리를 해보았는데요
이번글에서는 구현을 해보도록 하겠습니다!
구현할 예제는, 이제까지는 다루지 않았던 샘플인데요 꽤나 실제시스템과 비슷한 state space equation을 정의내리고 진행해보고자 합니다.

악필로 직접작성..
문제 정의는 이렇습니다.
어떤 사람이 인공위성을 향해 이동하고 있습니다.(100m/s + noise)
이런경우, 제가 가지고 있는 실측데이터는 오직1개 r(나와 인공위성사이의 직선거리)일때, distance, altitude, velocity의 추정값을 그려보는 문제입니다.
즉, 이런문제를 해결하기위해선 구해야하는 3개의 변수들과 r이 모두 각각서로 연관이 있어야겠죠?
일단 r = sqrt(distance^2 + altitude^2)입니다. 삼각형 대각선의 길이를 구하는 공식이죠
또한, altitude는 바뀌지 않는값입니다.
제가 어느위치에 있건 인공위성과 저와의 고도차이는 항상 유지되죠, 바뀌는것은 r값과 distance값입니다.
velocity는 간단하게 풀기위해 100m/s + noise로 주어보겠습니다.
요약하자면,
"등속도로 움직인다는 가정하에, r값은 실시간으로 센싱이될때 distance와 altitude를 예측해보라!")
가 미션입니다.

state space equation
일단, state space equation부터 세워보겠습니다.
distance = 속도*dt 이죠? 이부분을 위의 수식과 같이 matrix로 작성해보았습니다.
속도와 고도는 이전값 그대로이기에 별다른 추가항은 없고 위에서 구해진 matrix에 최종적으로
[1 0 0;0 1 0;0 0 1]인 Identity matrix를 더해주면 state-space equation은 완성입니다.
x_k = A * x_k-1에서 EKF에서는 A가 f(x)로 바뀌지만, 해당 state space eqaution은 f(x)는 선형이기에 A를 그대로 사용합니다.

h(x) jacobian
따라서, h(x)는 비선형입니다.
r = sqrt(x1^2 + x2^2)으로, altitude와 distnace를 통해, 나와 위성사이의 직선거리를 구해주고 noise를 넣어줍니다.(센서노이즈)
이것을 각각의 x값에대해 편미분하여 jacobian으로 정리를 해주면, 위의 이미지처럼 최종정리가 됩니다.
위의 예제를 UKF(Unscented Kalman Filter)를 통해 구현해보도록 하겠습니다.
sigma point는 7개(평균값 제외, 오른쪽/왼쪽으로 각3개씩)로 동작하는 코드입니다.

UKF로 위치,속도,고도를 추정해본 그림은 상기 이미지와 같습니다.

EKF로 추정했던 그림은 상기이미지와 같습니다.
altitude를 추정해가는 모습을 보면 뒷부분에서 EKF의 성능이 UKF가 좋은것을 확인할 수 있습니다.
물론, Case by Case로 이렇게 간단한 예제에서는 둘다 충분히 잘 동작한다는것을 확인할 수 있습니다.
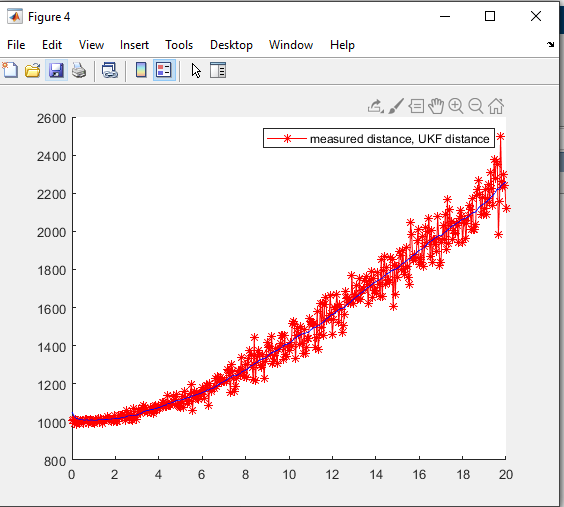

Distance(r) 추정은, Feedback제어로 돌아가는것이기에 둘다 높은 정확도와 비슷한 수준의 퍼포먼스를 보여주는것을 확인할 수 있습니다.
[코드분석-1]

UKF가 돌아가는 그림으로, EKF와는 전혀 차이가 없습니다.
[pos, vel, alt] = RadarUKF(r, dt);
[코드분석-2]

sigma points를 잡는 코드부분입니다.
n=3으로써, 2n+1 즉, 7개의 sigma points를 잡고있습니다.
각각의 Weighting(W) = 1/(2*(n+kappa))라는 수식으로 각 sigma point마다 다르게 웨이팅을 주고있습니다.
[코드분석-3]

Unscented Transform(UT)를 하는 부분입니다.
최종적으로 xcov인 P(Covariance),xm(Mean)값을 구해주는 부분으로써,
x_k의 sigma points들을 넣어서 얻어진 f(x_k)의 covariance와 mean값들을 정리해주는 코드입니다.
[코드분석-4]

이제까지의 예제들과 동일한 오차와 Noise를 주고, 센싱값을 정의하는 부분입니다.
[코드분석-5 : RadarUKF.m]
※이부분은 길이가 길어, 코드를 옮겨놓겠습니다.
function [pos, vel, alt] = RadarUKF(z, dt)
%
%
persistent Q R
persistent x P
persistent n m
persistent firstRun
if isempty(firstRun)
Q = [ 0.01 0 0;
0 0.01 0;
0 0 0.01 ];
R = 100;
x = [0 90 1100]';
P = 100*eye(3);
n = 3;
m = 1;
firstRun = 1;
end
[Xi, W] = SigmaPoints(x, P, 0);
fXi = zeros(n, 2*n+1);
for k = 1:2*n+1
fXi(:, k) = fx(Xi(:,k), dt);
end
[xp, Pp] = UT(fXi, W, Q);
%norm(xp - fx(x, dt))
hXi = zeros(m, 2*n+1);
for k = 1:2*n+1
hXi(:, k) = hx(fXi(:,k));
end
[zp, Pz] = UT(hXi, W, R);
%norm(zp - hx(xp))
Pxz = zeros(n, m);
for k = 1:2*n+1
Pxz = Pxz + W(k)*(fXi(:, k) - xp)*(hXi(:, k) - zp)';
end
K = Pxz*inv(Pz);
x = xp + K*(z - zp);
P = Pp - K*Pz*K';
pos = x(1);
vel = x(2);
alt = x(3);
%------------------------------
function xp = fx(x, dt)
%
%
A = eye(3) + dt*[ 0 1 0;
0 0 0;
0 0 0 ];
xp = A*x;
%------------------------------
function yp = hx(x)
%
%
yp = sqrt(x(1)^2 + x(3)^2);
: UKF의 전체적인 큰 알고리즘을 구현해놓은 코드입니다.
x_k 대표값(sigma points)추출 -> sigma points들을 f(x)에 통과시킴 -> f(x_k)의 mean과 variance를 구함 -> 칼만필터를 통해 [위치 속도 고도] 및 r(사람과 인공위성사이의 직선거리)를 추정해내는 것입니다.
Summary
UKF를 통해, 사람과 인공위성사이의 거리를 센싱하여, 인공위성과 지면사이의 고도, 및 나와 인공위성까지의 지면상 거리 및 속도를 추정해보는 예제를 구현해보았습니다.
UKF는 어렵지 않습니다. EKF도 마찬가지입니다.
Kalman Filter만 정확하게 이해하고 있으면 모두 파생적인 개념이기때문입니다.
각각에 대해 한줄요약을 해보자면
[칼만필터]
선형시스템을 칼만필터를 통해 여러가지 변수들을 추정하는 기법
[확장칼만필터]
비선형함수를 매 순간마다 미분해서 선형으로 근사시킨뒤, 칼만필터를 적용
[무향칼만필터]
대표값들 몇개를 비선형함수에 통과시키고 얻어지는 값들로 비선형함수값 그 자체를 추정해버린뒤, 칼만필터를 적용
입니다.
※ 참고
"칼만필터는 어렵지 않아" (2019,김성필)
'Control system engineering' 카테고리의 다른 글
| [제어시스템공학-12] Unscented Kalman Filter(UKF,무향칼만필터) 개념 (6) | 2021.02.03 |
|---|---|
| [제어시스템공학-11] Extended Kalman Filter(확장칼만필터) 구현 (6) | 2021.02.02 |
| [제어시스템공학-10] Extended Kalman Filter(확장칼만필터) 개념 (2) | 2021.02.01 |
| [제어시스템공학-9] Kalman Filter(칼만필터) 구현 - 실전예제 (0) | 2021.01.31 |
| [제어시스템공학-8] Kalman Filter(칼만필터) 구현 - 어려운예제 (0) | 2021.01.30 |




댓글