오늘 정리해볼 주제는 Average Filter(평균필터)입니다.
정말 간단한것부터 출발하는데요,
평균필터란 N개의 샘플이 있다고하면, N개를 모두 더하고 N으로 나누는것을 의미합니다.
즉, [1,2,3,4,5]라는 샘플들의 평균을 구하라! 라고하면, 흔히들 (1+2+3+4+5)/5=3 이라고 계산하는것 처럼요
이것을 그럴듯해보이게 "Filter" 라는 이름으로 한번 구현해보도록 하겠습니다.
이것은 (1+2+3+4)/4 * 0.8 + 5*0.2라고 볼수 있습니다.
즉, [1,2,3,4]가 들어온 현재상태에서 다음에 5가들어온다고 하면 1~4까지의 평균을 구해주고 (4/5)을 곱한뒤, 앞으로 들어올 5에 대해 (1/5)를 곱해주고 더해주면 결국 똑같은 3이 나오겠죠!
[ Ex ]
일반 자동차의 본네트 안에있는 배터리는 14V 부근입니다.
하지만, 어느날 노이즈(noise,잡음)가 심해서 10~18V까지 값이 널뛰면서 나온다고 전제를 해보죠
이런 경우에 1초단위로 총 100초간의 변화를 그래프로 그려보도록 하겠습니다.
필터가 잘 동작한다면 14V 부근에서 필터링된 값들이 쭉 찍히겠죠??

결과값을 보니 아주 잘 동작하는것을 확인하실 수 있습니다.
실제 측정된 Measured 값은 10~17V 인데 Average Filter를 통과하는 값은 뒤로갈수록 점차 안정을 찾아 14V로 수렴하는 모습이 보이네요!
즉, Noise를 제거하기에 Average Filter는 간단해보이지만 아주 파워풀한 퍼포먼스를 보여준다는것을 확인할 수 있습니다.
[1,2,3,4,5]를 모두 더해서 5로 나눈것도 평균이지만!
[1,2,3,4]의 평균 *(4/5) + 5 * (1/5)도 똑같은 평균입니다!
[1,2,3,4,5]의 평균 * (5/6) + 6 * (1/6)은 [1,2,3,4,5,6]의 평균과 똑같구요 :)
이것을 이해하는게 아주 중요합니다.
수식으로 표현해보면,
(1-a) * 이전까지의 평균 + a * 현재값 = Average Filter
라고 할수있겠네요.
즉, 이전까지의 값(x_k-1)이 현재 값(x_k)에 영향을 주는 구조인데요, 이것을 "Recursive(재귀)하다" 라고 표현합니다.
재귀적이지 않은 형태의 필터는 실전에서 "전혀" 쓸모가 없습니다.
따라서, 앞으로 정리해나갈 여러가지 종류의 필터들은 물론, 칼만필터까지 모두 Recursive한 특성을 가지고 있습니다!
[코드분석-1]

dt =1로 시간간격을 1초로 만든뒤,
t=0:dt:100으로 100초까지의 시간 샘플을 만들어준 모습입니다.
이어, Nsamples = length(t)로 샘플의 갯수를 100개루 맞추어 주고, xm과 avg라는 함수에 100개의 array에 해당하는 값들을 넣어줍니다.
① xm = getvolt() : getvolt라는 function을 읽어오는건데요, 뒤에서 설명하겠지만 14V에 noise를 준값들입니다.
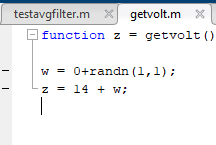
② avg = avgfilter(xm) : avgfilter라는 function이 평균필터의 본체이고, 필터링한 값들을 불러오는것입니다.
③ avgsaved(k) = avg;
xmsaved(k) = xm; : 위에서 불러온 측정값과 추정값을 array에 저장하는 코드입니다.
나머지는 plotting을 위한 코드입니다.
[코드분석-2]

avgfilter 함수입니다.
if isempty(firstrun) : 처음 초깃값을 선언하는 구문입니다.
① alpha = (k-1)/k;
: (1-a)*x_k-1 + a*x_k를 구할때의 a값을 구해주는 부분입니다.
② avg = alpha * preavg + (1-alpha) * x;
: average filter 본체입니다! ((1-a)*x_k-1 + a*x_k)
※ 참고
"칼만필터는 어렵지 않아" (2019,김성필)
'Control system engineering' 카테고리의 다른 글
| [제어시스템공학-5] Kalman Filter(칼만필터) 개념정리(2) (4) | 2021.01.27 |
|---|---|
| [제어시스템공학-4] Kalman Filter(칼만필터) 개념정리(1) (8) | 2021.01.26 |
| [제어시스템공학-3] Low Pass Filter(저주파 통과필터) (0) | 2021.01.25 |
| [제어시스템공학-2] Moving Average Filter(이동평균필터) (8) | 2021.01.24 |
| Control Engineering 정리에 앞서.. (0) | 2021.01.22 |




댓글