[Control Eng-1] Average Filter(평균필터) https://limitsinx.tistory.com/69
※이 전글에서 정리한 코드/문법은 재설명하지 않으므로, 참고부탁드립니다
※해당 글은 PC에서 보기에 최적화 되어있습니다.
오늘 정리해볼 주제는 Moving Average Filter(이동평균필터)입니다.
1번글 Moving Average에서 확인하셨다시피, 평균을 취하면 데이터의 잡음을 확실하게 처리할 수있습니다.
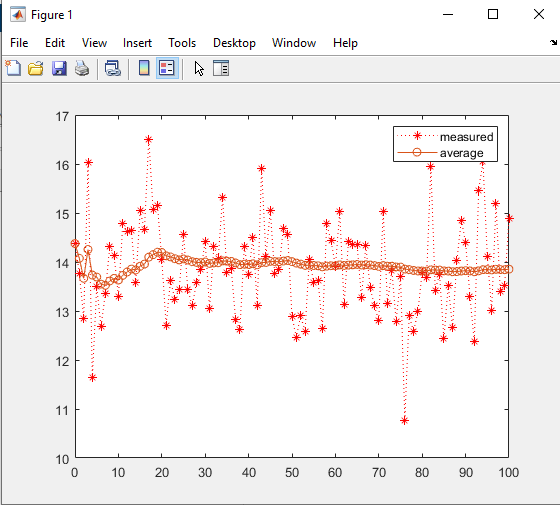
해당 예제는 측정하려는 값이 14라는 고정값이고, Noise가 껴서 들쑥날쑥한 경우였는데요
측정하려는 값이 지속적으로 바뀌는 경우라면, 단순한 Average Filter를 사용하는건 적절하지 않게 됩니다.
예를들어, 측정값이 1,2,3,4 .. 이렇게 1씩 늘어나는 경우라고 해보죠
이런경우 무작정, 전체 평균만 구하는식으로 필터링을 진행하게 된다면, 측정값을 뭉뚱그려놓은 값들만 계속 뱉어내게 되겠죠
즉, 실제 세계에 있는 대부분의 값들은 시간에따라 변하는값이기에 Moving Filter는 적용이 힘들다는 문제가 발생합니다.
Noise를 없앰과 동시에 측정값의 동적인 움직임을 제대로 따라갈만한 방법을 찾기위해 고안된것이 "Moving Average Filter" 입니다.
Average Filter는 현재까지 측정된 데이터들을 모두 더해서 그 갯수만큼 나누는 방식으로, 과거의 값들 전체의 평균이였다면,
현재 시점에서 과거의 일부분만 보면서 계속 평균을 구해나가는것이 Moving Average Filter입니다.
즉, [1,2,3,4,5]라는 input이 한개씩 차례대로 들어온다고 가정해보시죠
Moving Filter라면 이런값들이 나올것입니다.
1 -> (1+2)/2 = 1.5 -> (1+2+3)/3 = 2 -> (1+2+3+4)/4 = 2.5 -> (1+2+3+4+5)/5 = 3
[1,2,3,4,5]로 나와야 할 값들이 [1 1.5 2 2.5 3]이 나와버렸네요.. 이 Sequence의 길이가 길어지면 길어질수록 누적오차는 점점쌓이겠죠??
즉, 제대로 쫓아가지 못하고 있는상황인데요, 이번에는 Moving Average Filter로 확인해보겠습니다.
바로 직전값만 보고 따라간다고 가정해보시죠
1 -> (1+2)/2 = 1.5 -> (2+3)/2 = 2.5 -> (3+4)/2 = 3.5 -> (4+5)/2 = 4.5
| Measured | 1 | 2 | 3 | 4 | 5 |
| Average Filter | 1 | 1.5 | 2 | 2.5 | 3 |
| Moving Average Filter | 1 | 1.5 | 2.5 | 3.5 | 4.5 |
단순히 1씩 증가하는 예제만 들어도 이렇게, Filtering 성능에 차이가 남을 확인할 수 있습니다.
측정값의 Sequence가 길어지고, 값의 변동이 심해질수록 Average Filter의 한계는 더욱 극명하게 나올것입니다.

y=x+1 + noise를 주고 Average Filter로 쫓아가는 모습입니다.
점점 오차가 심해지는것을 확인하실 수 있는데요
똑같은 코드를 Moving Average로 따라가보겠습니다.

이전 5개의 값들의 평균만으로 지속적으로 y=x+1+noise를 따라가도록 설계를 한 Moving Average입니다.
Average Filter와는 확연한 차이가남을 확인하실 수 있습니다.
[코드분석-1]

이전 Average Filter 코드와 별반 다르지 않습니다.
xm = getvolt() 라는, 고정적인 14V에 Noise만 섞어준 것에서, y=x+1형식으로 getvolt_moving()이라는 함수로 작성해주었습니다.
1초간격으로 총 100개의 샘플에 Moving Average를 적용해보는 코드입니다.
[코드분석-2]

Moving Average 코드의 본체입니다.
n=5라는것은, 현재값 이전의 5개 데이터들에 대한 Moving Average를 취하겠다는 뜻입니다.
① xbuf = x*ones(n+1,1)
: 초기값(맨첫싸이클 돌때)으로는 [1 1 1 1 1] * input(x)를 지정합니다.
② for m=1:n
xbuf(m) = xbuf(m+1);
: 1~n까지 차례대로 들어온 값들을 계속 갱신해줍니다.
예를들면, [1,2,3,4,5,6,7]이 차례대로들어오는 경우,
[1,2,3,4,5] -> [2,3,4,5,6] -> [3,4,5,6,7] .... 이런식으로 5개씩 잘라서 움직이며 저장합니다.
③ xbuf(n+1) = x;
avg = preAvg + (x-xbuf(1))/n;
: [1,2,3,4,5] -> [2,3,4,5,6] 이 한가지예시만 봐주시기 바랍니다.
필터적인 관점에서 보면, 5개중 중간에 3개인 2,3,4는 그대로 있고, 첫번째 값(1)이 빠져나가고 새로운값이 1개(6) 추가되는 형태인것을 확인하실 수 있습니다.
이것이 x(새로운값) , xbuf(1)(첫번째값)에 대응되어, Moving Average의 평균인 avg를 구해주는 코드입니다.
※ 참고
"칼만필터는 어렵지 않아" (2019,김성필)
'Control system engineering' 카테고리의 다른 글
| [제어시스템공학-5] Kalman Filter(칼만필터) 개념정리(2) (4) | 2021.01.27 |
|---|---|
| [제어시스템공학-4] Kalman Filter(칼만필터) 개념정리(1) (8) | 2021.01.26 |
| [제어시스템공학-3] Low Pass Filter(저주파 통과필터) (0) | 2021.01.25 |
| [제어시스템공학-1] Average Filter(평균필터) (2) | 2021.01.23 |
| Control Engineering 정리에 앞서.. (0) | 2021.01.22 |




댓글