[Control Eng-1] Average Filter(평균필터) https://limitsinx.tistory.com/69
[Control Eng-2] Moving Average Filter(이동평균필터) https://limitsinx.tistory.com/70
[Control Eng-3] Low Pass Filter(저주파 통과필터) https://limitsinx.tistory.com/71
※이 전글에서 정리한 코드/문법은 재설명하지 않으므로, 참고부탁드립니다
※해당 글은 PC에서 보기에 최적화 되어있습니다.
오늘 정리해볼 주제는 "칼만필터"입니다.
제어공학에서 그 유명한 "루돌프 칼만"이 만들어낸 제어기법이죠
칼만필터는 일단 "선형시스템"에서는 최적화된 제어기법이라는 것이 수학적으로 증명되었습니다.
즉, 선형시스템을 다룰때는 칼만필터만 쓰셔도 될정도로 파워풀한 퍼포먼스를 보여주는 도구라는것입니다.
칼만필터는 전혀 어려운 개념이 아닌데요,
"칼만필터 수식"만 보고 어려움을 느껴 포기하는 분들이 대다수입니다.

처음 보시면 아마 "아.. 이거뭐야.. 이게뭐가쉬워.."라는 생각이 드실텐데요
수식만 복잡할뿐, 하나하나의 알파벳들이 가지는 의미가 별로 어렵지 않기때문에 금방정리할 수 있습니다!
또한, 칼만필터를 정리하기전 한가지 말씀드리고 싶은 부분은..
칼만필터를 처음부터 끝까지 수학적으로 유도를 하는 과정은 굳이 필요없으시다는것입니다!
굳이 시간나시면 해볼수도 있는데,
보통은 본인들의 연구분야에 이것을 "어떻게 사용할까?"를 주로 고민하신다고 생각합니다.
우리가 적분을 할때마다 매번 리만적분부터 유도를 하면서 사용하진 않죠, 보통 공식을 바로 떄려넣지
따라서 개념적인 부분은 꼭 알아두셔야할 부분만 확실하게 체크를 하고 자잘한 수학적 유도과정은 크게 집중하지 않도록 하겠습니다!

제가 가지고 있는 "칼만필터는 어렵지않아" 라는 책에 정리된 표입니다.
위의 칼만필터 수식보다는 훨씬 간결해졌죠??
저는 이 한장보다 칼만필터에 대해 잘정리된 글을 본적이 없습니다.
한번 따라가보겠습니다!
※ 각 알파벳위에 '-'가 있다면 "추정값" 이라는 의미이며, k는 현재스텝, k-1은 직전 과거스텝이라는 의미입니다.
① 초기값 선정
: 이전 스텝에서의 결과값이 그다음 스텝에서의 초깃값으로 들어갑니다.
즉, 이전 다른필터들에서도 다루엇듯 ,Recursive한 형태인거죠
② 추정값과 오차 공분산 예측
: 수식이 아주 어려워 보이시죠??
저렇게 복잡하게 적힌 수식들 중, 직접 구해야할것은 "P"밖에 없습니다.
A나 Q는 칼만필터로 계산하는게 아닙니다. 이미 정해져 있는 값입니다.
즉, 이전 상태에서 구한 P값에 이미 값이 다 정해진 A를 곱해주고 Q를 더해주어 현재상태의 P를 추측하는값을 구해주는것입니다. 그냥 산술문제입니다.
③ 칼만이득 계산(Kalman gain)
: 해당 수식도 H, R은 이미 칼만필터와 관계없이 정해진 값입니다.
즉, 2번에서 구한 "P"만 있으면 그냥 산술문제입니다.
④ 추정값 계산
: 이때까지 ①~③에서 구한값들과 센서로 측정한값(z_k)만을 가지고 현재상태의 값을 추정하는것입니다.
즉, 이것또한 산술문제입니다.
⑤ 오차공분산 계산
: ①~④에서 구한 값들로 오차공분산(P_k)를 구해주는것입니다. 역시 그냥 산술문제입니다.
여기서 구한 P_k는 다음 스텝의 ①로 돌아가 P_k-1이 됩니다.
정말 쉽지않나요??
위에 적힌 복잡한 수식에 관여된 알파벳들중 A,H,Q,R은 이미 정해진값입니다! 제가 신경쓸 필요가 없는거죠
나머지는 그냥 이미 정해진 A,H,Q,R로 숫자놀음 산술문제 푸는것이구요!
칼만필터가 어렵다 어렵다 하는데 이런 이미지를 보고 지레 포기해버리기 떄문입니다.

실상은 그냥 행렬 사칙연산만 할수있으면, 풀수있는 수준입니다.
그럼 요지는" A,H,Q,R이 뭔지만 알면!! 그냥 간단한 계산만으로 칼만필터를 구현할 수 있다" 라는것인데요
그럼 A,H,Q,R은 무엇을 의미할까요??
"What is A and H?"
A와 H는 State space equation(상태공간방정식)입니다.
제어공학을 한번도 배우시지 않은분들께서는 다소 생소한 개념이실텐데요,
현대제어공학은 state space equation의 전/후로 구분이 된다고 할정도로 아주 중요한 개념입니다.
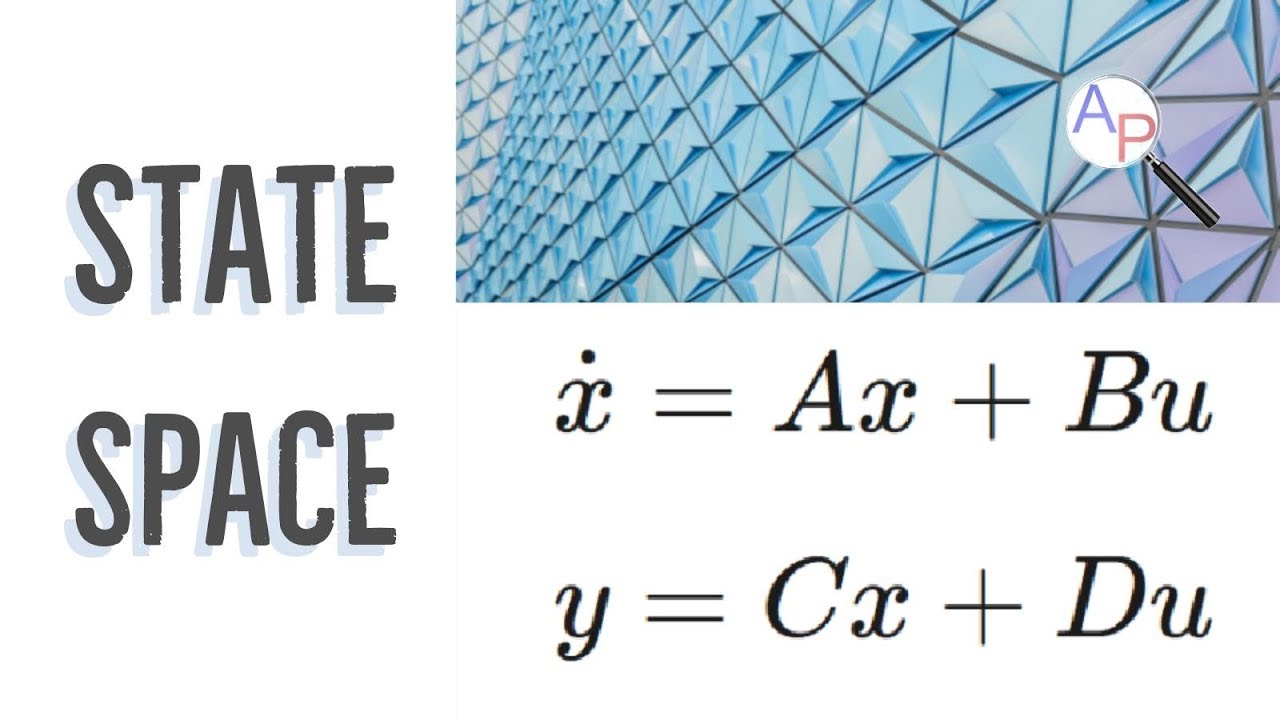
state space에 대해서만 다룬 책이 있을정도로, 해당 내용은 방대하고 깊게보자면 너무나도 깊은데요
짧게 요약해보도록 하겠습니다.
※일단 Q와 R은 무시하시고 넘어가셔도 됩니다.
[Ex] 등속도 운동을 하는 물체의 위치(이동거리) 찾기
x_k+1 = A*x_k + Q
z_k = H*x_k + R
이라는 수식이 있다고 가정해보시죠. x는 위치입니다.
등속도 운동을 한다는 전제가 있기에, x_k+1 = x_k 겠죠? x의 값은 언제나 동일할것입니다.
따라서 x_k=[위치;속도] 라는 2행 1열 벡터라고 했을때,
A= [1 △t;0 1]이 될것입니다.
왜냐구요? 한번 같이 구해보시죠
[현재위치;현재속도] = [1 △t;0 1]*[과거위치;과거속도] 가 x_k+1 = A*x_k의 의미입니다.
정리하자면,
현재위치 = 과거위치 + △t*과거속도
현재속도 = 과거속도
가되는것이죠!
이것이 바로 "A"입니다.
x의 변수간 관계를 통해 과거와 현재사이의 물리적인 수식을 행렬로 정리해놓은것이 바로 A입니다.
칼만필터를 구현하기위해선, 칼만필터가 어렵다기보다는 이 "A"를 얻어내는것이 어렵습니다.
본인이 적용하고자 하는 field에 대한 물리적/수학적인 이해가 필요하기 때문이죠(위의 간단한 예시처럼요)
감사하게도, 아래 링크처럼 state space equation에 대해 여러가지 물리적인 example들을 들어주며, 설명해주는 친절한 사이트가 있으니 공부를 하시는분들은 참고해주시면 좋을것 같습니다.
https://lpsa.swarthmore.edu/Representations/SysRepSS.html
State Space Representations of Linear Physical Systems
As systems become more complex, representing them with differential equations or transfer functions becomes cumbersome. This is even more true if the system has multiple inputs and outputs. This document introduces the state space method which largely
lpsa.swarthmore.edu
다음, H를 정리해보겠습니다.
z_k = H * x_k인데요 정말 간단합니다.
칼만필터는 어떤 센싱값(z_k)을 Reference(진리값)으로 삼고, 해당변수로 만들어진 상태방정식의 다른 값들을 지속적으로 구하는것입니다.
x_k = [위치;속도] 라면, 예를들어 속도센서가 있어서 정확한 속도를 항상 얻을 수 있다고 생각해보시죠!
현재위치 = 과거위치 + △t*과거속도
현재속도 = 과거속도
그럼 위에서 구한 'A'를 통해, 속도를 센싱한값으로 알게된다면, 위치는 덤으로 얻어지죠!
즉, [속도]만 알아도 [위치]를 알수있게 되는것입니다.
이것은, 위치-속도라는 아주 쉬운예를들어서 그런데요. state space equation을 아주 복잡하게 유도한다면, 아주 다른값을 구할수도 있습니다.
※ 예를들면, 제가 연구중인 배터리 모델링 분야에서는, 보통 전압(Voltage)값을 Reference로 잡고 배터리의 충전용량(SOC, State of charge)나 배터리 분극성분(Battery Polarization Voltage)를 칼만필터로 구하고 있습니다.
-정리하자면...
z_k = H * x_k에서 x_k = [위치;속도] 죠!
z_k는 센싱값이므로 위치를 센서로 측정하여 기준값으로 잡아 칼만필터를 연산하고 싶으면 H=[1 0]이 됩니다.
반대로, 속도 센서를 측정하여 기준값으로 잡고싶다면 H=[0 1] 이됩니다.
"What is Q and R?"
Q와 R은 바로 Noise입니다.
칼만필터는 시스템과 센싱값에 Noise(잡음)이 있다는것을 전제로, Kalman gain이나 공분산을 구하고 있는데요!
간단하게 생각하시면
세상에 아무리 완전무결한 퍼펙트한 센서가 있다 한들, Noise가 0일순 없을것입니다. 그것을 수식에 반영해주는것입니다. R로요
z_k = H*x_k + R
또한, 세상에 아무리 완벽한 state space equation이 있다한들, 세상을 수학으로 묘사한것이기 때문에 절대로 완벽하게 모든걸 표현할 순 없죠! 이것을 Noise라고 하여 수식을 반영해주는것입니다. Q로요
x_k+1 = A*x_k + Q
즉, R과 Q는 우리가 어떻게 할 수 없는 잡음(Noise)인데! 이 잡음의 생김새가 Gaussian distribution이라는 형태를 가진다고 가정하는 것입니다.

Signal Processing이나 Digital Communication/통신공학쪽을 전공하신분들이 익숙한 부분인데요
Noise는 보통 AWGN(Additional White Gaussian Noise)이라고 하여, "화이트 노이즈"를 일반적으로 사용합니다.
위의 그림과 같이 Gauss 형태를 가진 분포입니다.
왜 이것을 쓰는지에 대해서는 이제 이야기가 깊어지게 됩니다. Random Process라는 학문에 대한 이해가 필요하기 때문인데요
(이부분에 대해서만 대학강의 1달분량은 뽑을수 있을정도의 방대한 양입니다.., 심지어 random process는 한학기 교과목입니다..)
짧게 말씀드리면,
이세상에 존재하는 노이즈들중 많은 경우의수가 "Gaussian distribution"을 따르기 때문이라고 이해해주시면 됩니다.
따라서, Q는 사용자의 경험에 의해 어느정도 노이즈가 적절할지 임의로 결정하는 것이며
R은 센서의 노이즈이기에 대부분 센서제조사에서 이 값들을 주는 경우가 많습니다.
Summary
위의 글들을 통해, 칼만필터 연산과정은 아무것도 아닌것임을 정리해보았습니다!
A,H,Q,R이라는 변수들이 정해져있다면 칼만필터는 수식만 복잡해보일뿐, 결국 그냥 사칙연산으로 P(공분산), K(칼만이득)을 구하는것 뿐이었죠
여기서 A와H는 state-space equation으로 정리를 할 수 있으며, Q와R은 그냥 Noise(잡음)을 넣어준것일 뿐입니다.
여기까지 모두 이해되셨다면 칼만필터를 80%정도 이해했다고 보시면 됩니다.
다음글에서는 P와 K에대해 개념정리를 하여 나머지 20%를 모두 정리하고 바로 코드로 구현해보도록 하겠습니다!
※ 참고
"칼만필터는 어렵지 않아" (2019,김성필)
'Control system engineering' 카테고리의 다른 글
| [제어시스템공학-6] Kalman Filter(칼만필터) 구현 - 쉬운예제 (0) | 2021.01.28 |
|---|---|
| [제어시스템공학-5] Kalman Filter(칼만필터) 개념정리(2) (4) | 2021.01.27 |
| [제어시스템공학-3] Low Pass Filter(저주파 통과필터) (0) | 2021.01.25 |
| [제어시스템공학-2] Moving Average Filter(이동평균필터) (8) | 2021.01.24 |
| [제어시스템공학-1] Average Filter(평균필터) (2) | 2021.01.23 |




댓글