논문 전문 : https://ieeexplore.ieee.org/document/9895422
[출처] G. Cho, D. Zhu, J. J. Campbell and M. Wang, "An LSTM-PINN Hybrid Method to Estimate Lithium-Ion Battery Pack Temperature," in IEEE Access, vol. 10, pp. 100594-100604, 2022, doi: 10.1109/ACCESS.2022.3208103.
※ The picture and content of this article are from the original paper.
All picture and figures used in this article are sourced from publicily available on the internet.
[논문 요약]
An LSTM-PINN Hybrid Method to Estimate Lithium-Ion Battery Pack Temperature
요즘 관심있게 보고 있는 PINN(Physical Informed Neural Network)에 관한 연구 입니다.
일반적으로 PINN이라는 대명사로 지칭되는 연구의 초기는, 어떤 물성을 가지는 Product를 모델링함에 있어 PDE(Partial Differential Equation)하는 수고를 줄이고자, 이러한 부분에 ML/DL 방식을 접목하는것으로 시작되었습니다.
즉, 초기에는 뭔가 '대체제' 역할이 강했다면, 최근 연구 동향들과 제가 연구하고 있는 방향은 단순 대체제가 아닌, 모델 자체의 Adaptibility를 높일수있는 수단으로, 꼭 필요한 방식이라고 생각으로 접근하고 있습니다.
본 논문은, 그 중간즘 어딘가 위치하는 정도로 PINN을 적용한것으로 파악되며 저자중 한명이 Ford Engineer인데, EV에 강점을 보인다고 하기 어려운 회사에서도 내부적으로 이런 연구는 모두 진행하고 있구나라는 경각심을 일깨워주는 논문입니다.
Contents
본 논문의 Abstract에는 PINN을 '대체제와 Adaptibility'로 사용하고 있다고 말합니다. (Physics-based models for batery temperature prediction are often not suitable for online applications due to the large number of fitted parameters, how fidelity results from parameter inaccuracy and unaccounted model by dynamics.)

본 논문을 대표하는 이미지인데, 아쉽게도 PINN이라고하면 직관적으로 떠오르는 P2D모델과 같은 복잡한 배터리 모델에 적재적소에 AI를 삽입한 느낌은 전혀 아닙니다. 그냥 Loss function을 설계함에 있어 물리적인 의미를 조금 더 추가해서 학습이 되게 했을 뿐입니다.
이렇듯, 기존에는 모델 자체에 AI를 합성하려는 시도가 많았다면(Main목적이 모델 내 연산복잡도 저감이었으므로), 최근에는 Physical Equation만 따와서 Loss Function 혹은 Parameter에 세팅해주는 정도로도 PINN이라고 부르고 있습니다. 다소 예전의 정의보다는 희석된듯한 느낌이 강하게 듭니다.


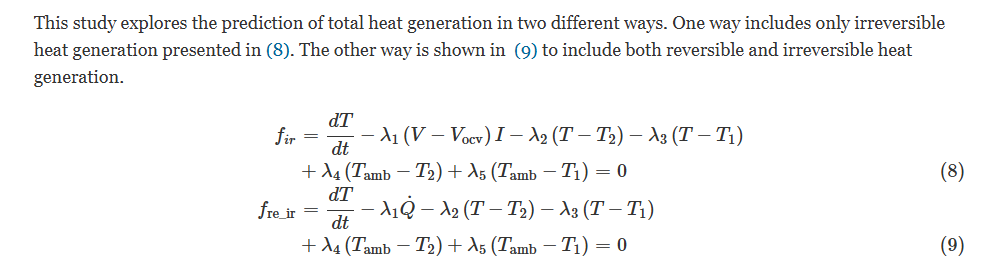
상기 수식(4)~(9)가 본 논문의 핵심입니다.
결국 본 논문의 주제는 "PINN을 활용한 온도 예측" 이기때문에, AI를 사용하는것이야 알겠고, Phyical Equation을 어떤식으로 AI에 녹여내느냐가 핵심이기 때문입니다.
배터리 발열량 연산 관련하여, 특이한 수식이 있진 않습니다. Irreversible Heat와 Reversible Heat을 각자 계산하고, 배터리 시스템의 여러 센서(T : Module Center TC, T1 : Pack Center TC, T2 : Pack Edge TC)들을 토대로 수식을 짜고, 이들을 토대로 학습이 되도록 각 항마다 lambda라는 Trainable Parameter를 설계해줍니다.

이를 통해 최종적으로 Loss는 상기와 같이 정의됩니다.
Loss_r은 예측한 온도와 실제 온도간의 차이이며, Loss_i는 Initial condition에 대한 것으로, 초기값에서 멀어질수록 Loss가 높게설계되어있습니다. 이는, 온도가 어떻게 변하냐도 중요하지만 첫 초기온도가 가장 중요하다는것을 학습시키기 위함으로 파악됩니다. Loss_f는 상기 수식(8),(9)에 대한 Loss 입니다. 이게 뭐냐면, 수식 (8),(9)를 자세히보시면 에너지 보존 법칙에 의해 최종적으로 각각의 f값들 합이 0이 되도록 설계되어있습니다. 즉, 에너지 보존 법칙에 따라 Lambda값들이 학습되고 0에 가까운 방향으로 학습되도록 설계한것입니다.
이부분은 꽤나 흥미롭고 인사이트 있는 신선한 방식이였습니다.

상기 수식대로 정리된 PINN은 위의 그림과 같이 학습됩니다.
T, T1, T2 3개의 온도를 추정하도록 학습되며, 최종적으로 PINN을 통해 T를 예측하도록 설계됩니다.
단순 LSTM을 통해 T1, T2를 예측하고, 이 예측값이 다시 PINN의 입력으로 들어가서 재학습되도록 특이하게 구성해놓았는데요, 여기서 학습에 사용되는 Inputs Data는 (Time, Current, Voltage, OCV) 입니다. 이 변수들은 모두 Reversible, Irreversible Heat를 구하는데 필요한 변수들입니다.

챔버 Ambient Temperature도 추가하게되면 상기와 같이 Network가 설계됩니다.


저는 본 논문에서 가장 저와 의견을 같이하는 부분이 상기 그림이라 생각합니다.
개인적으로 Reversible Heat에 대해서는 매우 의구심이 많이듭니다. (물리적으로 의미가 있지만, 온도를 Sweep하면서 얻는다는 부분이 저는 개인적으로 오래걸리기도하고 이렇게해야하나 라는 생각이 듭니다.)
본 논문에서도 이에 대한 의견 합치로 Reversible Heat를 빼고 해봤는데, 결과가 상당히 잘나오는것을 확인하실 수 있습니다. 온도별로 OCV를 찍는 엄청나게 수고가 많이드는 일을 하지 않고도 거의 동일한 수준의 정확도를 보인다는점에서 제 생각이 틀리지 않았구나 라는것을 데이터로 확인할 수 있는 계기가 되었습니다.
Results
생각한 PINN은 아니였지만, 수식들이 전개적으로 짜임새있게 설계되어있고 결과물 또한 좋았습니다.
Reversible Heat에 대한 의견도 저와 유사했고, 특히 수식(8),(9)와 같이 에너지 보존 법칙을 기반으로 Physical Raw를 따르는 발열량 추정 수식을 짰다는 점에서 아주 인사이트가 있었습니다.
참조
[1] G. Cho, D. Zhu, J. J. Campbell and M. Wang, "An LSTM-PINN Hybrid Method to Estimate Lithium-Ion Battery Pack Temperature," in IEEE Access, vol. 10, pp. 100594-100604, 2022, doi: 10.1109/ACCESS.2022.3208103.




댓글