논문 전문 : https://www.sciencedirect.com/science/article/abs/pii/S037877531931290X
[출처] Bernhard Liebhart, Lidiya Komsiyska, Christian Endisch,Passive impedance spectroscopy for monitoring lithium-ion battery cells during vehicle operation,Journal of Power Sources,Volume 449,2020,227297,ISSN 0378-7753, https://doi.org/10.1016/j.jpowsour.2019.227297.
※ The picture and content of this article are from the original paper.
[논문 요약]
Passive impedance spectroscopy for monitoring lithium-ion battery cells during vehicle operation
명작은 결과를 알고서도 다시보게 만든다는 구절이 생각나는 논문입니다.
본 논문은 이전에도 정리한적이 있으나, 문득 생각이나서 최근 다시 읽은 논문입니다.
Driving Vehicle operation이라 되있는데, SAE에 개제된 어떤 논문에서는 컨버터/인버터에서 발생하는 주파수성분을 가지고 EIS를 추저한다고했으나 이 논문은 그런건아니고 충방전의 복잡한 주행프로파일 내에서 주파수 임피던스 성분을 추정하는 논문입니다.
Contents
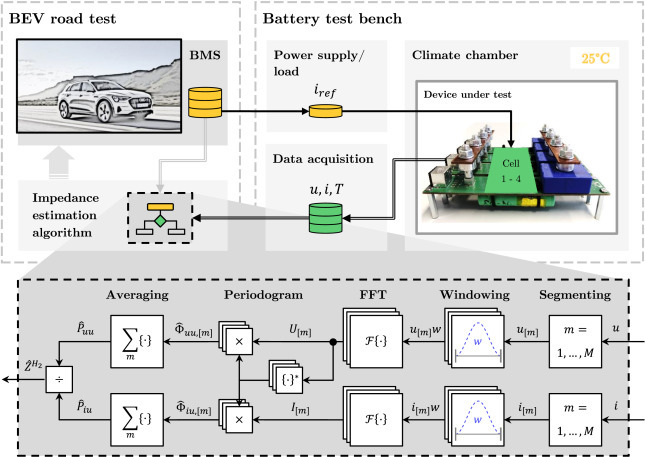
본논문의 알파이자 오메가입니다.
EV 주행데이터는 △I 변화량이 엄청나게 큽니다. 급가속과 회생제동이 반복되며 나타나는 형태이기에 이러한 전기적 Flow속에서 유의미한 주파수 성분을 찾아내서 임피던스를 추정해보겠다는것이 본 논문의 핵심입니다.
일반적으로 EIS라고하면, Lab Scale에서 AC Osciliator 장비를 가지고 정밀한 센싱을 기반으로 mHz~kHz단위까지 직접 배터리의 입력으로 인가해주고 나오는 출력을 통해 임피던스를 추정하는 경우가 많습니다.
이건 근본적으로 Lab scale밖에 할수없는 큰 네가지 이유가있습니다.
첫번째, 금전적 문제입니다. 테슬라의 경우 (21700 기준) 약 7000개의 원통형 셀이 들어가는데요, 각 배터리 셀들의 EIS를 찍자고 센서 7000개를 추가로 탑재할수는 없습니다. 또한, 배터리 시스템의 패키징 특성상 병렬연결된 부분들은 전압센서를 통일하는 경우가 많기때문에 더더욱 불가하다고 볼수있습니다.
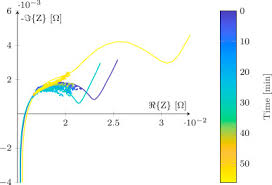
두번째로는, 배터리 셀 특성 그 자체입니다. Lab Scale의 전극 장수가 적은 코인셀 혹은 소형셀에서는 상기와 같이 Nyquist Plot이 예쁘게 그려질 수 있습니다. 하지만, 실제 양산에 활용되는 어마어마한 용량/에너지의 배터리 셀은 측정장비를 가지고 Nyquist Plot을 그리더라도 이렇게 예쁘게 그려지지 않습니다.
세번째로는, 측정환경입니다. Lab Scale에서는 온도도 균일하고, 발열도 억제하고(소형셀이니까), C-rate도 균일하게해서 측정을합니다. EIS는 특히 온도에 민감한 결과물을 산출해내기때문입니다.
하지만 EV,ESS처럼 배터리 '셀'이 아닌 '시스템' 단위로 가게되면 이러한 조건을 만들어줄수가 없습니다.
당연히 CC(Constant Current)로 운영되지 않을뿐 아니라, 발열이 심하고, EV나 최근 데이터센터에서 수냉식으로 쿨링을 하기때문에, 최대한 균일한 냉각을 해주려하지만 시스템 내에 온도 분포가 생기게될수밖에 없습니다. 즉, 배터리 시스템 내에 각각의 배터리 셀들의 환경도 모두 달라진다는 점입니다.
네번째로는, 센서 샘플링 성능입니다. 배터리 컨트롤러 입장에서는 Discrete Time에 대한 주파수해석이 필요하기에, 센서의 시간분해능이 절대적으로 중요합니다. EIS가 러프하게 1mHz~1kHz까지만 요구한다고하더라도 시간도메인에서는 0.5ms이하의 샘플링 성능이 필요합니다. 이는 가격경쟁력을 고려해야하는 양산제품에는 적용하기 불가능한 수준의 수치입니다.

본 논문도 이러한 4가지 문제점을 해결하진 못했으나, 그래도 "비슷하게라도" 어떻게든 임피던스를 추정해보자 라는 마음이 느껴졌습니다. 이를 위해 상기와 같이 한번의 DFT(Discrete Fourier Transform)이 아니라 여러번의 Segment 그리고 이 Segment간에도 Overlap을 하면서 특정 주파수 성분에 대해 최대한 균일한 값이 나오도록 하는 시도가 있었습니다.
본 논문에서는 이걸 WOSA 알고리즘이라 부르던데, 시계열 딥러닝하는분들한테는 이런 Window로 Segment를 나누는 데이터 전처리는 아주 일상적인것입니다.

그리고 KK라고하여 Kramers-Kronig 방식을 통해 추정한 임피던스값들에 대한 Extrapolation을 수행합니다. 이 기법은 Passive EIS에서 많이 사용되는 방식으로, 저는 별로 관심이 없는 분야이지만 데이터의 내/외삽을 목적으로 많이 사용되는 방법중 하나입니다.
결국 전체를 정리해보자면, WOSA 방식과 DFT를 통해 특정 주행프로파일에 대한 주파수-임피던스를 추정하고, KK를 통해 데이터를 내/외삽하며 상기와 같은 Nyquist Plot 추정치를 그려냅니다.
결과를 보면, 꽤나 유사하게 나오는것을 확인할 수 있으며, 본 논문에서는 40microseconds 수준의 시간 샘플링(이것도 비현실적임.)을 했기에 Nyquist Plot의 반원부분을 어느정도 추정할 수 있는것을 확인할 수 있습니다.
저는 이 논문을 완벽한 Nyquist Plot을 그리기위한 Passive EIS방식이라고 생각하면 실망하실수 있을것으로 추정됩니다. 다만, 저는 완벽한값 보다는 경향성(Trend)를 파악할 수만 있는 하나의 Index라도 충분하다 라고 생각하기때문에 상당히 만족스러운 논문이였습니다.
Results
이런 방식의 주파수 임피던스 추정논문은 꽤나 있으나, 논문의 전체적인 흐름을 봤을때 가장 매끄러운 논문이 아닌가 싶습니다. 언제봐도 맛있는 논문입니다.
참조
[1] Bernhard Liebhart, Lidiya Komsiyska, Christian Endisch,Passive impedance spectroscopy for monitoring lithium-ion battery cells during vehicle operation,Journal of Power Sources,Volume 449,2020,227297,ISSN 0378-7753, https://doi.org/10.1016/j.jpowsour.2019.227297.




댓글