논문 전문 : https://www.mdpi.com/1996-1073/13/8/2057
[출처] Energies 2020, 13(8), 2057; https://doi.org/10.3390/en13082057
※ The picture and content of this article are from the original paper.
[논문 요약]
An Accurate Time Constant Parameter Determination Method for the Varying Condition Equivalent Circuit Model of Lithium Batteries
배터리 Equivalent Circuit Model에 대해서는 거의 정형화되어있는 기술이기에 특별히 색다를건없다라고 생각하고있던찰나, 본 논문은 꽤나 신선한 인사이트를 던져주었습니다.
필드 적용 여부를 떠나, Circuit Relay ON/OFF를 구분하여 다르게 모델링한것이 재미있는 논문으로, 굳이 이렇게까지? 싶지만서도 대학교에서 나온 논문이기에 연구목적으로는 신선해보였습니다.

Contents

본 논문은 1RC-ECM에서 Relay를 on/off 했을때의 전압거동특성에 대해 다르게 모델링을 한것입니다.
일반적으로는 회로가 연결(Realy on)되어있다는 전제하에 하기와 같이 Terminal Volage를 수식화하는데요

일반적으로는 크게 고려하지않던 Realy off때까지 하기와 같이 수식화했습니다.
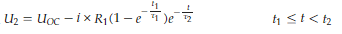
여기서 재미있는점은 시상수를 구하는 공식인 Resistance * Capacitance에서 Resistance를 구할때의 회로 해석을 신기하게 한다는점입니다.


부하 상태에서 시상수를 구하기위해 저항을 구하는데, 이것을 커패시터의 관점으로 해석해버립니다.
(a)그림에서 1//2라고 적힌곳이 원래 커패시터자리입니다. 무부하상태에서 커패시터에 차있는 전압이 빠지는것 성분만 있다고 가정하고, 여기서 커패시터의 시선으로 R0,R1,R2를 보면 R0, R2는 직렬연결되어있고 R1과는 병렬연결되어 있는 형태입니다.
따라서 커패시터 관점에서는 회로의 전체 저항이 R_eq1처럼 됩니다.
이렇게해서 시상수(tau_1)을 구하고, 부하중에는 하기와 같이 일반적으로 알려진 방식대로 구합니다.

아무래도 무부하시 전압 곡선을 추정하는 Relaxation Model도 별도로 연구가 되고있는만큼, 부하/무부하시에 발생하는 Polarization, Diffusion 같은 화학반응에서의 차이점을 각자 반영하고자 이런식으로 설계한것으로 추정됩니다.
다만, 커패시터는 양방향소자로 충/방전이 복합된 EV Driving Pattern에서는 용이하지않을뿐만 아니라, 온도/열화에 대해서는 고민하지 않은것은 조금 아쉬웠습니다.
그리고, 논문의 Figure가 하기와 같이 잘못그려진부분이 있어 읽기가 어려웠습니다.

Results
Capacitor의 관점에서 ECM의 부하상태를 구분하여 모델링한다는 점이 재밌었습니다.
하지만, 논문의 검증과정에서 하기와 같이 HPPC 형태의 파형으로만 수행했는데 실제 ESS/EV Profile로 검증도 해봤으면 더욱 좋았을것 같습니다.

참조
[1] Energies 2020, 13(8), 2057; https://doi.org/10.3390/en13082057




댓글