논문 전문 : https://ieeexplore.ieee.org/document/9254622
[출처] C. Chen, G. Yesilbas, A. Lenz, O. Schneider and A. C. Knoll, "Machine learning approach for full impedance spectrum study of Li-ion battery," IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, 2020, pp. 3747-3752, doi: 10.1109/IECON43393.2020.9254622.https://doi.org/10.1016/j.apenergy.2014.01.066.
※ The picture and content of this article are from the original paper.
[논문요약]
Machine learning approach for full impedance spectrum study of Li-ion battery
몇가지 대표 포인트의 배터리 EIS값을 측정하고, 포인트들 사이의 Interpolation을 머신러닝 기법을 통해 최적화하여 측정한 EIS와 동일한 형태의 Nyquist Plot을 얻고자 하는 논문입니다.

Purpose
위의 이미지와 같은 Nyquist Plot을 얻기위해 대표성을 띈다고 필자가 정한 5개의주파수(20mHz, 5Hz, 200Hz, 2kHz)를 측정하고 그 사이의 간격들을 머신러닝 기법을 통해 부드럽게 이어가는게 목표입니다.
논문제목에서 머신러닝이라 적혀있어, Neural Network를 사용하는 줄 알았지만 그건 아니고 오히려 수치해석적 기법인 Low Rank Factorization을 통해 대표 포인트들 사이의 Interpolation을 진행합니다.

즉, 붉은색 포인트들 사이의 파란선을 머신러닝을 통해 최대한 실제 EIS 결과값과 부드럽게 이을 수 있도록 하는것입니다.
Contents
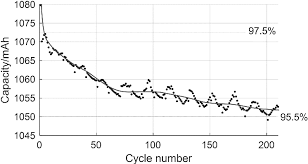
학습하기 위한 데이터 축적을 위해, 210Cycle의 실험을 진행합니다.
초기 1회는 1C-rate 충/방전이며, 이후 4C-rate 충/방전 실험을 하며, 초기 10회 사이클은 매번 실험이 끝날때마다 EIS를 측정하고 이후에는 10회의 사이클마다 한번씩 EIS를 측정합니다.
아쉽게도 Dynamic한 환경에서는 동작하지 않으며, SOC 100%에서 Relax된 상태의 배터리 임피던스를 측정합니다.
Nyquist Plot을 정확히 그리기위해서는 0.5mHz ~ 20kHz의 주파수범위가 필요하지만, 필자는 본인의 판단하에 20mHz ~ 2kHz면 충분히 필요한 영역은 그릴 수 있다고 하여 논문을 진행합니다.
저는 1mHz ~ 10kHz는 찍어야 한다고 생각하는데 조금다르네요
필자가 선택한 5개의포인트에 맞는 주파수들을 sine wave로 만들어 동시에 배터리의 Input으로 인가하고 임피던스를 계산합니다.

머신러닝 기법으로는 Low Rank Matrix Factorization을 사용합니다.
수치해석적 접근으로 이것에 대해서는 차후 자세하게 정리해보고, 해당 논문을 이해하기 위한 정도로만 정리를 해보겠습니다.
A라는 Matrix와 동일한 값을 가지는 두개의 Matrix의 곱을 만들고싶다고 가정해보면
A(5,5) = B(5,1) * C(1,5)로 만들어줄 수 있겠죠
즉 5행-5열의 Matrix가 5행-1열 및 1행-5열의 낮은 Dimension의 Matrix의 곱으로 분해될 수 있다는 것입니다.
A는 목표값이기에 이미 정해진 Matrix이면, B의 한 행을 모두 b로두고, C의 한 열을 모두 c로 둔다고 가정해봅시다.
그리고 A-(B*C) = 0이 되도록 수치해석적으로 b와 c를 바꿔가면서 계속 반복하면 어느지점에서 A-(B*C)가 최솟값이 되는 b와 c가 나오게 될것입니다.
이것을 최적화된 b와 c값으로 볼 수 있는것이죠
해당 논문은 여기서 b와 c가 대표 포인트 5개 이외 중간중간 interpolation해야하는 지점들의 값입니다.
이런식으로 반복하여 interpolation을 진행 한 결과, 다른 여러 보간법들 대비 실제 EIS 개형을 더 잘따라갔다는것이 해당 논문의 내용입니다.

빨간색이 EIS로 실측한 값이고, 남색선이 LR Decomposition으로 interpolation하며 따라간 개형입니다.
다른 보간법들 대비 가장 잘따라가는것을 확인할 수 있습니다.
자세히보시면, 추가적으로 5개의 포인트를 추가하여 총 9개포인트를 선형으로 따라가는것을 확인할 수 있습니다.
Results

결과적으로 다른 3가지 유명한 interpolation 방법대비, Low Rank Matrix Factorization을 통한 interpolation이 가장 EIS개형을 잘 따라가더라 라는 결론으로 끝이납니다.
위의 그래프는 각 방법들에 대한 실측값과의 RMSE 값입니다.
눈에띄게 ML이 오차가 낮은것을 확인할 수 있습니다.
이런식으로도 EIS 개형을 따라갈 수 있다는 논문으로는 아주 괜찮은것 같지만, LR-Decomposition의 연산 복잡도나(다차원에서 SVD를 해야함) 여러 배터리의 제약적인 상황에서의 따라가는 정도이기에, 어떤 실제 Load가 걸리는 배터리에는 사용하기 힘들지 않을까라는 아쉬움이 있었습니다.
참조
1. C. Chen, G. Yesilbas, A. Lenz, O. Schneider and A. C. Knoll, "Machine learning approach for full impedance spectrum study of Li-ion battery," IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, 2020, pp. 3747-3752, doi: 10.1109/IECON43393.2020.9254622.https://doi.org/10.1016/j.apenergy.2014.01.066.




댓글