[pytorch 따라하기-1] 구글 Colab에 pytorch 세팅하기 https://limitsinx.tistory.com/136
[pytorch 따라하기-2] Tensor생성 및 Backward https://limitsinx.tistory.com/137
[pytorch 따라하기-3] 경사하강법을 통한 선형회귀 구현 https://limitsinx.tistory.com/138
[pytorch 따라하기-4] 인공신경망(ANN) 구현 https://limitsinx.tistory.com/139
[pytorch 따라하기-5] 합성곱신경망(CNN) 구현 https://limitsinx.tistory.com/140
[pytorch 따라하기-6] Neural Style Transfer 구현 https://limitsinx.tistory.com/141
[pytorch 따라하기-7] pix2pix 구현 https://limitsinx.tistory.com/142
[pytorch 따라하기-8] DC-GAN(Deep Convolutional GAN) 구현 https://limitsinx.tistory.com/143
※이 전글에서 정리한 코드/문법은 재설명하지 않으므로, 참고부탁드립니다
※해당 글은 PC에서 보기에 최적화 되어있습니다.
"RNN(Recurrent Neural Network)?"

한때 CNN과 더불어 시대를 풍미하던 모델인, RNN에 대해 정리해보도록 하겠습니다.
시계열(Time Sequential)데이터를 학습하는 경우, 필요한 모델인데요. 제가 주로 다루는 모델입니다.
이제까지 General한 Neural Network부터 CNN까지, 모든 데이터들은 Time과 연관되어있지 않았습니다.
즉, 이미지 수만장(MNIST) 혹은 데이터들을 학습시켰을뿐이지, 이게 시간적인 연관성을 전혀 가지진 않았다는 말이죠
예를들면..
"H E L L O" 라는 단어를 자동검색어에 뜨도록 학습시키고 싶다고 가정을 해보시죠
그럼 H라는 단어를 쳤을때 E L L O라고 다음 값이 나올 수 있도록 학습이 되어야겠죠
그럼 기존의 학습방법은 input 한 알파벳을 치면, 그 다음 알파벳이 나오도록 학습을 하는것입니다. 아래처럼요

H -> E
E -> L
L -> L
L -> O
이렇게 1개의 input을 주었을때 다음 output으로는 그다음 알파벳이 나오도록만 학습을 해주는것입니다.
그런데 이상한게 보이시죠??
똑같은 Input을 주었는데 다른 output이 나와야하는 경우가 발생하는 것입니다.
즉, "L이 2번연속나왔을때는 O라는 output을 주도록해라~" 라는 새로운 학습조건이 필요하게 된거죠
이게바로 Time Sequential Data(시계열데이터) 입니다. 이전 과거의 값이 현재의 값에 영향을 미치는거죠
이런 데이터들을 학습시키기 위한 것이 바로 RNN 입니다.
현재 state에서의 x_t(input)과 h_y(hypothesis)로 y_t를 만들어내는것이, 이제까지의 Neural Network 였다면,
과거의 x_t-1, h_t-1, y_t-1이 현재의 y_t를 구성하는데까지 모두 영향을 주는것이라는 거죠

손으로 하나씩 공책에 적어가면서 따라 가다보면 이해가 훨씬 쉽습니다.
개념적인 부분에 대해 정리를 하기위해 Notation을 정리해보겠습니다.
[Notation]
x_(t-1) : 과거의 input 데이터
y_(t-1) : 과거의 output 데이터
h_(t-1) : 과거의 hypothesis
W_(t-1) : 과거의 Weighting
b_h : 과거의 Bias
W_hh : 과거의 Hypothesis를 현재로 넘길때 곱해지는 Weighting
x_t : 현재의 input 데이터
y_t : 현재의 output 데이터
h_t : 현재의 hypothesis
W_xh : 현재의 Weighting
W_hy : 현재의 State와 과거의 Hypothesis를 통해 y_t를 얻기위해 곱해지는 Weighting
b_t : 현재의 Bias
tanh : activation function(기존의 ReLU, sigmoid ...와 같은 활성함수)
[개념정리]
과거의 데이터부터 정리해보겠습니다.
h_(t-1) = W_(t-1)*x_(t-1) + b_(t-1) 입니다.
y_(t-1)은 해당 State에서의 Weighting과 Bias값들이 더해진것이므로, 이 다음 State필요한것은 y_(t-1)이 아닌, 좀더 본질적인 값인 h_(t-1)입니다.
따라서, h_(t-1)은 W_hh와 곱해져 다음 State로 넘어가게 됩니다.
이부분이 아래 빨간 네모박스 부분의 동작개요 입니다.

이것으로 과거데이터의 값은 모두 정리되었습니다. (W_hh * h_(t-1) + b_h)
현재 State로 가보겠습니다.
h_t = W_xh * x_t + b_t 입니다.
여기에 과거의 값을 더해줌으로써 최종적인 현재 state에서의 h_t가 완성됩니다.
h_t = W_xh * x_t + W_hh * h_(t-1)
이것을 Activation Function인 tanh에 통과시킨후, W_hy를 곱하고 bias를 더해주면 최종적으로 현재 state에서의 y값인 y_t 가얻어집니다!
y_t=W_hy * tanh(h_t) + b_t
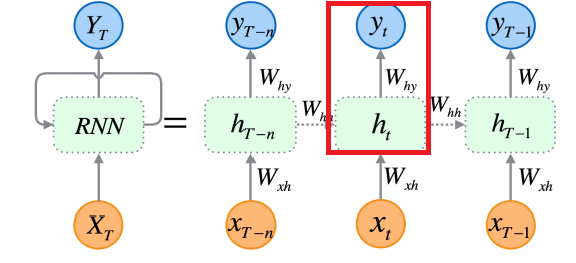
즉, 빨간 네모박스 친 부분이, 위에서 현재 state를 기준으로 정리한 값들입니다.
이렇게하면 감이 조금 오는것이, 기존에는 x_t와 관계된 y_t만이 나왔는데
x_(t-1)을 토대로 연산한 h_(t-1)이 관여된, y_t를 얻게 되죠!
즉, 과거의 데이터가 현재의 상태에 영향을 미치게 되는것으로, 이것을 "RNN"이라고 부릅니다.
"LSTM(Long Short Term Memory)"
RNN은 과거의 데이터값들을 기억하지만, Layer가 Deep해질수록 점점 과거의 값들이 "희석"되는 문제가 발생합니다.
즉, 일반적인 Neural Network에서 발생했던 "Vanishing Gradient"와 같은 문제가 생기는거죠

예를들면, t-1의 값들은 t 상태에서 잘 가지고 있지만, t-100의 값은 거의 영향력이 없게 될것입니다.
따라서, 과거의 데이터들이 희석되는 문제점을 고쳐준 것이 바로 "LSTM(Long Short Term Memory"입니다.

상기 그림의 첫번째 이미지가 RNN 두번째가 LSTM인데요
RNN은 위에서 설명한바와 같이, h_(t-1) + W_hx*x_t 를 tanh에 통과시킨채로 해당 Layer에서의 연산이 종료됩니다.
하지만, LSTM에서는 과거의 값을 좀 더 잘 보존할 수 있도록 내부적으로 여러가지 연산장치들을 추가해놓았습니다.
(망각/입력/출력 게이트라는 세개의 게이트를 현재의 데이터와 한스텝전 Hidden state를 기반으로 연산하여 현재 Hidden state와 출력값을 도출하는 시스템입니다. 수식은 복잡해보이지만, 손으로 수식을 따라가보면 별것 아닙니다..)
즉, RNN의 Process Sequence를 따르되, Cell은 "LSTM"이라는 독특한 내부구조를 적용시켜주는것입니다.
- 하기 이미지는 LSTM의 "Cell" 내부를 수식화해서 정리해놓은 것입니다.


코드
# Created by Hyunjun,JANG
# limitsinx.tistory.com
# Last revision date : 2021.08.03
import numpy as np
import pandas as pd
import pandas_datareader.data as pdr
import matplotlib.pyplot as plt
import datetime
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# GPU setting
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#print(torch.cuda.get_device_name(0)) #Google colab = TESLA T4
# Training/Test ratio = 7:3
Train_ratio = 0.7
Test_ratio = 0.3
# Data load
df = pd.read_csv('/content/sample_data/california_housing_train.csv')
x = df.iloc[:,0:-1]
y = df.iloc[:,-1:]
# Data Division
train_x = x.iloc[0:int(len(df)*Train_ratio),:]
train_y = y.iloc[0:int(len(df)*Train_ratio),:]
test_x = x.iloc[int(len(df)*Train_ratio):,:]
test_y = y.iloc[int(len(df)*Train_ratio):,:]
# Normalizing , 둘다 학습하여 성능비교할것
minmax = MinMaxScaler()
standard = StandardScaler()
train_x = minmax.fit_transform(train_x)
train_y = minmax.fit_transform(train_y)
test_x = minmax.fit_transform(test_x)
test_y = minmax.fit_transform(test_y)
# Check Data pre-processing
#print("Training shape : ", train_x.shape, train_y.shape)
#print("Test shape : ",test_x.shape, test_y.shape)
# Numpy array상태로는 학습이 불가능하므로, Torch Variable 형태로 변경(data/grad/grad_fn)
train_x_tensor = Variable(torch.Tensor(train_x))
train_y_tensor = Variable(torch.Tensor(train_y))
#print("After torch variable shape_Train : ",train_x_tensor.shape, train_y.shape)
test_x_tensor = Variable(torch.Tensor(test_x))
test_y_tensor = Variable(torch.Tensor(test_y))
#print("After torch Variable shape_Test : ",test_x_tensor.shape, test_y_tensor.shape)
train_x_tensor_final = torch.reshape(train_x_tensor, (train_x_tensor.shape[0], 1, train_x_tensor.shape[1]))
train_y_tensor_final = torch.reshape(train_y_tensor, (train_y_tensor.shape[0], 1, train_y_tensor.shape[1]))
test_x_tensor_final = torch.reshape(test_x_tensor, (test_x_tensor.shape[0], 1, test_x_tensor.shape[1]))
test_y_tensor_final = torch.reshape(test_y_tensor,(test_y_tensor.shape[0], 1, test_y_tensor.shape[1]) )
#print(train_x_tensor_final.shape, test_x_tensor_final.shape)
# LSTM network modeling
class LSTM_Jun(nn.Module):
def __init__(self, num_classes, input_size, hidden_size, num_layers, seq_length) :
super(LSTM_Jun, self).__init__()
self.num_classes = num_classes
self.num_layers = num_layers
self.input_size = input_size
self.hidden_size = hidden_size
self.seq_length = seq_length
self.lstm = nn.LSTM(input_size = input_size, hidden_size = hidden_size, num_layers = num_layers, batch_first = True)
self.layer_1 = nn.Linear(hidden_size, 256)
self.layer_2 = nn.Linear(256,256)
self.layer_3 = nn.Linear(256,128)
self.layer_out = nn.Linear(128, num_classes)
self.relu = nn.ReLU() #Activation Func
def forward(self,x):
h_0 = Variable(torch.zeros(self.num_layers, x.size(0), self.hidden_size)).to(device) #Hidden State
c_0 = Variable(torch.zeros(self.num_layers, x.size(0), self.hidden_size)).to(device) #Internal Process States
output, (hn, cn) = self.lstm(x, (h_0, c_0))
hn = hn.view(-1, self.hidden_size) # Reshaping the data for starting LSTM network
out = self.relu(hn) #pre-processing for first layer
out = self.layer_1(out) # first layer
out = self.relu(out) # activation func relu
out = self.layer_2(out)
out = self.relu(out)
out = self.layer_3(out)
out = self.relu(out)
out = self.layer_out(out) #Output layer
return out
# Code Main
num_epochs = 10000
learning_rate = 0.001
input_size = int(len(x.columns))
hidden_size = 2 # number of features in hidden state
num_layers = 1
num_classes = int(len(y.columns))
LSTM_Jun = LSTM_Jun(num_classes, input_size, hidden_size, num_layers, train_x_tensor_final.shape[1]).to(device)
loss_function = torch.nn.MSELoss()
optimizer = torch.optim.Adam(LSTM_Jun.parameters(), lr = learning_rate)
for epoch in range(num_epochs) :
outputs = LSTM_Jun.forward(train_x_tensor_final.to(device))
optimizer.zero_grad()
loss = loss_function(outputs, train_y_tensor.to(device))
loss.backward()
optimizer.step() # improve from loss = back propagation
if epoch % 200 == 0 :
print("Epoch : %d, loss : %1.5f" % (epoch, loss.item()))
# Estimated Value
test_predict = LSTM_Jun(train_x_tensor_final.to(device)) #Forward Pass
predict_data = test_predict.data.detach().cpu().numpy() #numpy conversion
predict_data = minmax.inverse_transform(predict_data) #inverse normalization(Min/Max)
# Real Value
real_data = train_y_tensor.data.numpy() # Real value
real_data = minmax.inverse_transform(real_data) #inverse normalization
#Figure
plt.figure(figsize = (10,6)) # Plotting
plt.plot(real_data, label = 'Real Data')
plt.plot(predict_data, label = 'predicted data')
plt.title('Time series prediction')
plt.legend()
plt.show()
결과물

인터넷에서 돌아다니는 다변량 회귀 데이터 중, 집값 예측 Kaggle데이터를 가져와서 학습시켜보았습니다.
파란색이 실제 집값이고, 주황색이 예측된 값인데요, epoch을 1000번정도 밖에 안했지만 상당히 괜찮은 성능이 나오는것을 확인할 수 있었습니다!
'DeepLearning Framework & Coding > Pytorch' 카테고리의 다른 글
| [Pytorch-11] Auto Encoder (0) | 2021.08.14 |
|---|---|
| [Pytorch-10] One Class SVM(Support Vector Machine, OCSVM), SVDD (2) | 2021.08.11 |
| [pytorch 따라하기-8] DC-GAN(Deep Convolutional Generative Adversarial Network) 구현 (0) | 2021.07.27 |
| [pytorch 따라하기-7] pix2pix 구현 (0) | 2021.07.27 |
| [pytorch 따라하기-6] Neural Style Transfer 구현(이미지 합성) (2) | 2021.07.26 |




댓글